2025_BUAA_OO_Unit1

第一单元的OO在紧张与刺激中落下帷幕，回顾第一单元，真是应了吴际老师上学期在OOPre的最后讲的“一定要好好理解文法分析，不然下学期的第一单元会很痛苦”。整个Unit1就是围绕文法展开，前前后后就是让我们展开表达式，在我们做好这个蛋糕后，再用化简优化去为它裱花点缀。

第一次作业

第一次作业较为简单，因为出现的是最基本的常数与幂函数，且括号最多一层，因此实现起来并不困难，只要把词法和语法分析做好，并能实现展开，第一次作业就基本成型。

1.1程序架构

UML类图

功能说明

• Main：程序入口
• Expr、Term、Variable、Const：表达式的基础结构
• Symbol：进行符号处理，保证每一个项的内部不会出现正号或负号，且每个项前最多有一个符号
• Lexer、Parser：进行语法和词法分析
• Poly：把项规范为形如 的形式
• Operate：进行运算，包括表达式幂的展开和项的展开

1.2代码复杂度

可以发现，其中Operate、Parse、Symbol的复杂度比较高，其中有最大的圈复杂度甚至达到了16。我在这几个类里面所用到的条件判断语句和循环语句以及函数调用比较多，因此造成了圈复杂度比较高。拿Symbol类举例来说，虽然里面就只有两个方法，但针对字符串化简符号的逻辑是十分复杂的，尤其是项里面有子表达式的时候，因此涉及到很多判断和循环，造成圈复杂度很高，而这样的结果也说明了我这个类以及里面的方法其实可迭代性和可维护性并不好，因为化简符号不像词法和语法分析那样只需要添加一定的token和语法解析就能实现，在后续表达式逐渐变复杂后整个符号化简的逻辑可能会大变，而且遇上多层嵌套括号后复杂度可能会很高。
进一步分析，其实会发现我第一次作业的架构和”高内聚低耦合”似乎不太沾边，我后续作业是经过了重构的，因此后续完全没有回顾过我第一次作业。而当我重看第一次作业代码时，抛开写得shi不shi不谈，其实理解还是很容易理解的，但是整体看下来其实好像并不是在写面向对象编程，而是在写面向过程编程，很多类的耦合度过高，而有的类该自己干的事没干，不该自己干的事干了，甚至有的类干的事和自己的名字都没啥关系，比如Poly。因此我在第一次作业结束后发现在这样的代码基础上迭代十分困难，决定重构。

1.3化简优化

能把整个表达式正确展开后，其实本次作业的正确性我们已经可以拿满分了，但是估计性能分会很低。针对第一次作业，其实化简无非就是同类项合并，而判断能否合并也十分简单，只需要判断展开后每个项中x的幂次相等，最后如果所有项里有符号为正的，我们把它放在第一位即可省掉一个负号带来的长度，实现了这些后，性能分也可以拿满。

1.4Bug分析

在互测中我出现了一些WA的错误，而错误的来源全是来自于我Symbol类中化简符号的方法出错（其逻辑真的很复杂，bug修复时针对这一个bug都修改了好多行），具体出错的原因是我把项里子表达式的第一个符号拿出来给了整个项，若是正号还好，但如果是负号，我整个项的符号就会取一次反，最终造成错误。
事实上，这个符号简化的方法完全是自己折腾自己，因为完全可以把符号放在语法分析里面一起，这样在解析完一个项时，它的符号也被解析出来，因此我后续重构的时候完全摒弃了这一个类。

第二次作业

第二次作业较第一次作业的难度陡然上升，引进了三角函数和自定义递推函数，同时允许多层嵌套括号。主要有两个难点，一个是如何正确地算出递推函数并代入表达式，一个是针对有三角函数的化简可以怎么做，如果不考虑化简的话，只需要解决递推函数这个难点即可。由于第一次作业我的架构很烂，层次不清淅，因此第二次作业我首先进行了重构。

2.1程序架构

UML类图

功能说明

• Main：程序入口
• Expr、Term、Var、Const、Trigono、Func：表达式基础结构
• Parser、Lexer、Token：语法词法解析
• Funcrecur：递推函数相关信息获取，并计算递推函数
• Regofunc：存储被解析出来的递推函数规则，供整个项目使用
• Bracketdeal：括号处理，寻找匹配的括号
• Equandneg：判断表达式是否相等或相反
• Unit：最终表达式中的最小单元，形如
• Entirety：由多个Unit组成的单元

2.2代码复杂度

在本次项目中，复杂度较高的类为Unit类，其他类复杂度稍高可能是因为条件和循环语句稍多，例如Lexer和Bracketdeal类，而Unit类的复杂度是由于其里面涉及了很多方法，包括运算以及判断是否能合并等方法，涉及到的方法调用也较多，因此呈现了一个较高的复杂度。
此次作业我尽可能的满足了“高内聚低耦合”的想法，尽可能把一些特定功能单独抽象出来成为一个类，同时尽量保证每个类只干和自己相关的事。
重构前后对比
先抛开本次作业新增的三角函数和自定义递推函数不谈，其他部分我也和第一次作业有很大的差别。
首先是词法和语法解析，本次我单独设计了一个Token类，里面包含了字符串所包含的可能的字符类型，而不是在Lexer类里对字符串中的一个一个字符分析，整理来说可理解性和可迭代行会增强不少。我还在Parser里面确定了项的符号，直接抛弃了第一次作业中的Symbol类，且这样的方法几乎适用于往后的所有迭代。
其次我设计了Entirety和Unit两个类，最终的计算化简全都在这两个类中进行，而所有的表达式基础结构如Expr等都有一个toentirety()方法，方便之后的展开和化简，这样，我的代码在面临下一次迭代时可能不需要修改很多东西就能适应情景，而层次化的结构也比较清晰，这提高了整个项目的可维护性。

2.3难点分析及化简优化

前面说到，本次作业主要有两个难点：一个是递推函数，一个是三角函数化简。
针对递推函数，我采用字符串替换的方式，替换字符串后再对得到的字符串进行一次词法和语法分析并重复操作直到表达式中不含形如“f{n}(x)”的东西。要注意的是，在这里替换字符串的时候为了以防错误替换，可以先把第i个参数用“ai”替换，全部替换完后再将对应的“ai”替换为真正的实参。
针对三角函数的化简，其实难点在于如何判断两个三角函数是否相等或相反，也即三角函数内部的表达式是否相等或相反。这里我采用了一种比较暴力的方式，我想既然我们整个程序做的事情就是化简表达式，那我要判断两个表达式是否相等或相反，是不是可以把这两个表达式相加或相减，然后调用我们的程序其是否为零即可。综合各方面性能考虑，我最后决定只做 ， ，以及正弦函数二倍角的化简，而且为了使最终结果的长度尽可能短，我在最后一步才化简，以防出现本来可以合并但在中途化简之后无法合并的情况。

2.4Bug分析

此次作业我出现了一些RE和WA以及TLE的错误，其中最主要的是RE错误。RE的原因是我在做递推函数的字符串替换时，忽略了可能嵌套函数的情况，导致我用的逗号下标可能是嵌套函数里面的逗号的下标，最后替换的结果自然是错的，为了修复这个问题，我添加在Token中添加了Comma这一类型，这样就能准确找到属于当前函数的逗号的下标，从而正确替换字符串。
而WA和TLE的原因在于我在合并Unit时，需要判断每个三角函数的幂次是否相同，但是我的三角函数在Unit里是用HashMap<String,Integer>来存储的，我对幂次相同的判断直接用的等号，但是显然等号是不适用于Integer内容的判相等的，因此出现了错误，当我改用Objects的equals方法后，问题就解决了。

第三次作业

第三次作业添加了自定义普通函数和求导算子，自定义普通函数的处理方法和第二次作业的自定义递归函数的处理方法类似，而且更简单，只不过由于函数内部的因子多了自定义普通函数这一选项，在替换和解析的时候可能需要做一点改动。而关于求导，可以采用自下而上的方法，先把最基本的常数、幂函数和三角函数的求导实现，再实现项和表达式的求导。本次作业我在第二次作业的基础上进行迭代，添加的东西并不多。

3.1程序架构

UML类图

新增类和功能

• Deriva：表达式基础结构，表示求导因子
• Funcparse：新增解析普通函数功能
• Regofunc：新增了两个普通函数规则
• Parser、Lexer、Token：新增对求导因子的解析
• 各类基本单元：新增求导方法

3.2代码复杂度

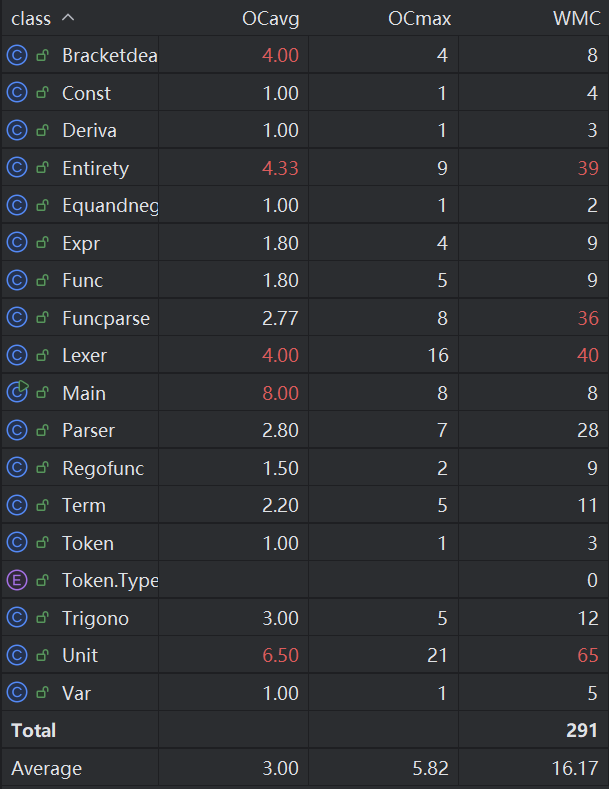
本次复杂度和第二次作业类似，但由于我把读取字符串的行为放在了Main类里，而这次读取字符串需要读普通函数，因此条件语句可能会增多导致圈复杂度上升。

3.3Bug分析

本次作业出现了几个RE和WA的错误。
RE是由于我在解析递推函数的参数个数时是靠逗号的个数来计算的，而此次由于递推函数表达式中可以出现普通函数，因此很可能会得到错误的参数个数，针对此问题，我修改为只考察等号左边是否有逗号，这样可以省去对右边复杂的分析。
WA是由于我没有考虑嵌套求导的情况，我原本的Deriva类里有toentirety()和derivative()两个方法，但这两个方法完全一样，因此导致嵌套求导时该求多次导的表达式只求了一次导，针对该问题，我将toentirety()方法修改为求一次导，将derivative()方法修改为求两次导，这样便修复了Bug。

TalkTalk

程序优缺点总结

仅针对重构后的程序（重构前的优点是写的复杂）
优点

• 层次清晰，类设计合理，基本实现高内聚低耦合
  缺点
• 代码写得有点冗余，有些部分可能出现了好几次，这时应该把其抽象出来为一个方法
• 性能不够优秀，判断表达式相等或相反直接调用整个程序，在嵌套很深的时候会出现卡死的情况，可以考虑重写Hashcode来方便判断。
• 没有实现更多的化简，这也主要是由于对判相等方法性能的担忧，若修改了判想等方法，应该能实现更多化简。

新迭代情景

加入指数函数以及自定义分段函数（自定义分段函数内的因子一定满足在某个确切的自定义分段范围内，比如常数因子，或者表达式（x^2-2*x+1）等）。
针对指数函数较好实现，只需新增一个实现接口Factor的类，并添加相应的求导方法即可。
针对自定义分段函数需要新增解析其规则的方法，而若因子为常数，只需判断其在哪个区间并代入相应函数表达式即可，对于含变量x的因子，可以新建一个方法（直接代值计算）去判断其属于哪个区间并代入相应函数表达式。

hack策略

这三次作业我都成功hack到了同组的同学，尤其是第三次几乎将组内所有同学都hack了。我的策略是自己设计数据，从简到繁，且充分考虑特殊情况。拿第三次作业来说，我先从sin(0)^0这样的数据开始，然后到求导，设计一些可能出错的求导样例去验证大家求导实现得是否正确，最后添加函数，并考虑嵌套函数等情况。
可能有部分同学用评测机来进行该环节，单个人认为数据生成器生成的数据随机性过大，可能运行很久也没有一个有效的样例能hack到别人，而如果是生成了十分复杂的数据造成同学tle，可能又会因为cost的限制而难以修改到能够成功提交。但我认为评测机针对我们自己查自己bug还是十分重要的，尤其是针对强测环节，而这也是由于其生成数据的随机性。

心得体会

1）Don’t be reckless

我们拿到一个题目或需求或想法时，不应一上来就开始敲键盘，这样不计后果的行为是十分危险的，没有经过充分的理解题目和需求，没有经过充分地思考，没有经过精心的设计，直接开始写代码很大概率会写出一个极难阅读、理解和维护的怪物。而且当你写着写着很可能会想起好像还有什么需求没有实现又去修改前面写的代码，这样在写的过程中不断的进行修改，写程序本应是伴随修改的，但应该是负责任的修改，是考虑过的修改，而不是鲁莽随意的修改。因此，在开始写代码前，我们应该对自己的架构有了一个基本的认知，清楚的知道自己的需求和目标是什么，这样才能使整个项目层次尽可能清晰，方便后续的阅读和修改。

2）be careful

谨慎，既在思考设计时，又在编写程序时，还在回顾修改时。在三个阶段都应该保持谨慎的心态，尽可能去思考自己的程序是否有什么情况还没有考虑到。我便是忽略了这一点，写完总是认为自己的程序应该没什么问题了，导致强测常会出一些错误。

3）be stern

这里我不是想说要认真的意思，我想表达的是我们可以逼自己一把，对自己狠一点，做一做自己不敢做的事，比如化简，做一做自己不想做的事，比如重构，做了这些，我们首先会积累到相应的经验，总结到方法，能提升自己的能力，还能进一步加强对架构的理解，理解某种架构为什么好，好在哪里。

4）be exclamatory

我在unit1经常感叹别人的设计，别人的方法，无论是上机时发给我们的代码还是往届学长学姐们的博客以及讨论区大家的发言，很多时候我都会想起余华老师评价莫言老师那句“**，写得那么NB”。学习和运用这些架构和方法，也让我的代码变得更好，让我逐渐学会怎么写出优雅的代码，让我对项目设计有了更深的理解。我认为本单元交给我最重要的方法就是递归下降法，但交给我最重要的思想是架构设计的思想，什么时候该分一个类，类里面该干什么事，怎样降低不同类之间的耦合度，怎样让项目可维护性更好……我在上学期除了OOPre之外还修了一门java程序设计，那门课的大作业是写一个工作量为2000行代码的程序，我写了一个创新的贪吃蛇游戏，其实逻辑并不复杂，但由于涉及到GUI，仍然需要去设计相应的架构，设计不同的面板之间的关系，不同类中的方法，但我当时写得很杂，几乎是每一关就对应了一个类，很多该抽象出来的方法和类并没有抽象出来，导致代码非常冗余，且修改起来也十分头疼，当时为了修复一个很奇怪的bug找了半天对应的代码位置。所以我是真的十分感叹unit1中遇到的所有设计和方法，当然不能止于感叹，还要运用，化为自己的东西才有用。

建议

• 可以介绍一下项目的度量分析的各类指标分别是什么，是由什么决定的，反映了什么，这样能让大家在度量分析后对自己的代码有更深的认识
• 提交hack数据时可以返回给我们提交数据的相应cost，这样在cost超过限制时，我们能够好地去修改数据